Câu 5. Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\). Tập hợp các điểm \(M\) sao cho \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)

(A) Mặt cầu có tâm là trọng tâm của tam giác \(ABC\) và bán kính bằng \({{a\sqrt 2 } \over 2}\).

(B) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \({{a\sqrt 2 } \over 4}\).

(C) Mặt cầu có tâm là trọng tâm của tứ diện và bán kính bằng \({{a\sqrt 2 } \over 2}\).
(D) Mặt cầu có tâm là trọng tâm của tam giác \(ABC\) và bán kính bằng \({{a\sqrt 2 } \over 4}\).

Giải

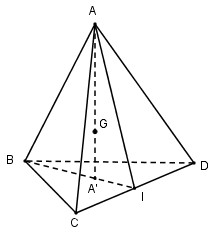
Gọi \(G\) là trọng tâm tứ diện \(ABCD, AA’\) là đường cao xuất phát từ \(A\) của tứ diện \(ABCD\). Ta có:

\(\eqalign{
& AA' = \sqrt {A{B^2} - BA{'^2}} = \sqrt {{a^2} - {{{a^2}} \over 3}} = {{a\sqrt 6 } \over 3} \cr
& \Rightarrow GA = GB = GC = GD = {3 \over 4}AA' = {{a\sqrt 6 } \over 4} \cr} \)

Ta có:   \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = 2{a^2}\)

\(\eqalign{
& \Leftrightarrow {\left( {\overrightarrow {GA} - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GB} - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GC} - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GD} - \overrightarrow {GM} } \right)^2} = 2{a^2} \cr
& \Leftrightarrow 4G{A^2} + 4G{M^2} - 2\overrightarrow {GM} \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 2{a^2} \cr
& \Leftrightarrow M{G^2} = {{{a^2}} \over 2} - G{A^2} = {{{a^2}} \over 8} \Rightarrow MG = {{a\sqrt 2 } \over 4} \cr} \)

Tập hợp các điểm \(M\) là mặt cầu tâm \(G\) bán kính \({{a\sqrt 2 } \over 4}\) . Chọn (B).